Research
Thermo-chemical structure of Earth’s mantle
Our main goal is to directly infer Earth’s mantle composition and thermal state from a broad range of geophysical data, including seismic, gravity, geodetic and electromagnetic sounding data, that sense disparate physical rock properties. The present approach results from recent advances in seismic tomography and mineral physics, particularly knowledge of elastic properties of mantle phases at high pressure and temperature, that have spurred an increased interest in the origins of the observed lateral variations in physical properties (seismic wave speeds, density and electrical conductivity) of mantle and crustal minerals. Rather than invert for the physical property to which a specific geophysical field gives rise to, we jointly invert different geophysical fields for composition and thermal state. Compared to conventional geophysical inversion techniques, our strategy has the advantage of providing a natural way of integrating the widely different data sets. At the same time, it also allows us to obtain tighter constraints on the inverted parameters. These improved constraints are realized by combining thermodynamic modeling of mantle mineral phase equilibria with inversion of geophysical data using stochastic sampling methods. These results obtained provide us with the information that is crucial to unravel the relative importance of chemical and thermal contributions that are observed as variations in seismic wave speeds in tomographic images. In turn, this information will provide constraints on the dynamic evolution of the Earth.
Six models of the thermal and compositional structure of the mantle lithosphere beneath North America obtained from stochastic inversion of surface-wave dispersion data. From Khan et al. (2011).
Publications
The Thermo-Chemical and Physical Structure beneath the North American Continent from Bayesian Inversion of Surface-wave Phase Velocities, Khan, A., Zunino, A. and Deschamps, F., J. Geophys. Res., accepted for publication, 2011. [pdf]
Mapping the Earth's thermochemical and anisotropic structure using global surface wave data,
Khan, A., Boschi, L. and Connolly, J. A. D., J. Geophys. Res., 116, B01301, doi:10.1029/2010JB007828, 2011. [pdf]
On Mantle Chemical and Thermal Heterogeneities and Anisotropy as Mapped by Inversion of Global Surface Wave Data, Khan, A., Boschi, L. and Connolly J. A. D., J. Geophys. Res., 114, B09305, doi:10.1029/2009JB006399, 2009. [pdf]
Composition, origin and evolution of the terrestrial planets
Intimately related to the outstanding and still much debated question of mantle chemical stratification is the question of the possible building blocks of the terrestrial planets, and in particular of the Earth and the terrestrial planets. The composition of peridotites, which are samples from the upper mantle and have been used to infer its composition, are found to be depleted in Si relative to the chondrites. The latter are traditionally thought of as the building blocks of the terrestrial planets, as the chondrites appear to sample the primitive material that started out as dust in the solar nebula and which grew, through collisional processes, into planets. A possible solution to the conundrum of Si depletion, then, is to propose that it has been sequestered into the core and/ or lower mantle. The resolution of the lower mantle Si content, or the bulk mantle composition in general, thus holds the potential of providing insight into the nature of the material from which the Earth assembled. Using various types of geophysical data (e.g. seismic, electromagnetic sounding and geodetic data), we have been able to provide certain
constraints on the average composition of the Earth, the Moon and Mars. For example, for the Earth we found that (Khan et al., 2008):
the lower mantle in contrast is found to be enriched in FeO and depleted in SiO2,
with a Mg/Si ratio of ~1.2 and a Mg# of ~0.83, resulting in a bulk silicate Earth
composition that is unmatched by any of the common chondrites,
while for Mars (Khan and Connolly, 2008):
The most probable bulk Fe/Si ratio is ~1.2, indicating that Mars most probably
accreted from material with a nonchondritic (CI) Fe/Si ratio, such as the ordinary
chondrites (L and LL), which also have oxygen isotopic ratios matching those in
Martian meteorites.
These interdisciplinary studies benefited greatly from working closely with geochemists and petrologists, notably John Maclennan, Stuart Ross Taylor and James Connolly.
Publications
Inversion of seismic and geodetic data for the major element chemistry and temperature of the Earth's mantle, Khan, A., Connolly J. A. D. and Taylor, S. R., J. Geophys. Res., 113, B09308, doi:10.1029/2007JB005239, 2008. [pdf]
Constraining the Composition and Thermal State of Mars from an Inversion of Geophysical Data Khan, A. and Connolly J. A. D., J. Geophys. Res., 113, E07003, doi:10.1029/2007JE002996, 2008. [pdf]
Are the Earth and the Moon Compositionally Alike? - Inferences on Lunar Composition and Implications for Lunar Origin and Evolution from Geophysical Modeling
Khan, A., Maclennan, J., Taylor, S. R. and Connolly, J. A. D., J. Geophys. Res., 111, E05005, doi: 10.1029/2005JE002608, 2006. [pdf]
Electromagnetic sounding and electrical conductivity
Electromagnetic sounding (EM) of the Earth has proven a valuable geophysical tool in addition to seismology for probing the physical structure (electrical conductivity) of Earth's mantle. In spite of EM soundings having lower spatial resolution in comparison to seismic methods, they are an important complement to the latter for extracting information on the physical state of Earth's mantle. In principle, electrical methods provide stronger constraints on chemical composition and thermal state because electrical conductivity is more sensitive to variations in mantle chemistry and temperature and hence on mineralogy, than do elasticity properties. Using electrical conductivity as a means to infer the amount of water stored in the upper mantle and transition zone is of particular interest as even small amounts of water can cause signicant changes to the physical properties of mantle minerals with potentially strong implications for mantle dynamics. This work has been done in collaboration with Alexey Kuvshinov, Nils Olsen and Thomas Shankland.
Laboratory mineral electrical conductivity measurements as a function of inverse temperature. (a) Upper mantle. (b) Transition zone. (c) Upper part of lower mantle. (d) Variations in mineral phase proportions and laboratory‐based conductivity profile computed on the basis of a homogeneous adiabatic pyrolite mantle as a function of pressure (depth) and transition zone water content are shown in Figures 9b and 9d. The solid and dotted lines in Figure 9d are bulk conductivity and adiabat, respectively. From Khan et al. (2011).
Comparison between inverted profiles (same as in Figure 6) and laboratory‐based profiles for various adiabats (red, 1200°; blue, 1300°; green, 1400°; and transition zone water contents). For all laboratory‐based profiles shown, we assume, as in Figure 9, a homogeneous pyrolitic mantle composition. For comparison, some previous laboratory‐based conductivity models are shown from the studies of Xu et al. [2000a] (magenta), Khan et al. [2006] (yellow), and Yoshino et al. [2008a] (solid black). Note that the model by Khan et al. [2006] is the mean profile, and uncertainties (not shown) are typically of the order of ±0.5 S/m, while the model of Yoshino et al. [2008a] was only constructed between 200 and 800 km depth. From Khan et al. (2011).
Publications
A geophysical perspective on Earth's mantle water content: Inverting long-period electromagnetic sounding data using laboratory-based electrical conductivity profiles
Khan, A. and Shankland, T. J., Earth Planet. Sci. Lett., submitted, 2011. [pdf]
On the Heterogeneous Electrical Conductivity Structure of the Earth's Mantle with Implications for Transition Zone Water Content
Khan, A., A. Kuvshinov and A. Semenov, J. Geophys. Res., 116, B01103, doi:10.1029/2010JB007458, 2011. [pdf]
Constraining the Composition and Thermal State of the Mantle beneath Europe from Inversion of Long-period Electromagnetic Sounding Data
Khan, A., Connolly, J. A. D. and Olsen, N., J. Geophys. Res., 111, B10102, doi:10.1029/2006JB004270, 2006. [pdf]
Constraining the Composition and Thermal State of the Moon from an Inversion of Electromagnetic Lunar Day-Side Transfer Functions
Khan, A., Connolly, J. A. D., Olsen, N. and Mosegaard, K., Earth Planet. Sci. Lett., 248, doi:10.1016/j.epsl.2006.04.008, 2006. [pdf]
Inverse problems
Inverse problems are a cornerstone in geophysics and much of the geosciences. Solving an inverse problem means making inferences about some model from observations. The general inverse problem could be formulated as d = g(m), where d is a data vector, m is an unknown model parameter vector and g is a generally non-linear operator (physical law) that connects d to m. The fully non-linear (here referred to as the general inverse) problem is typically characterised by one or both of the two following items: 1. data can only be computed from a model by means of a numerical algorithm and/or 2. the a priori model constraints can only be expressed using numerical algorithms. Whereas for linear and 'weakly nonlinear problems', which can be locally linearised, analytical methods can provide estimates of the best fitting model and measures of resolution (nonuniqueness of uncertainty), this is not possible for general inverse
problems. Instead we have to rely on stochastic-based sampling algorithms such as MCMC to collect information on the posterior probability density in the model space. The most widely employed sampling methods are the Metropolis algorithm and the Gibbs sampler. The method renders sampling of the posterior probability density possible, even in cases where the prior information is only available as an algorithm that samples the prior probability density. Given a collection of models sampled according to the posterior, we can proceed to estimate posterior model parameter covariances or resolution measures that are more useful in many applications, such as evaluating posterior probabilities for the existence
of structures in the Earth or planet of interest. Application of sampling-based methods and analysis using Bayesian tools have been applied extensively to lunar geophysical data (e.g. seismic, geodetic and electromagnetic souding data). Much of this work was done in close collaboration with Klaus Mosegaard.
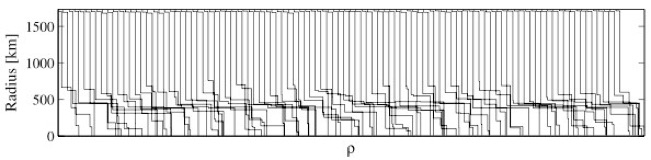
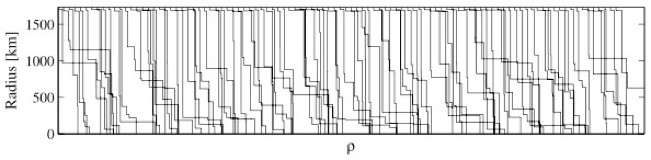
Samples of the lunar density structure obtained from inversion of lunar geodetic data. One hundred samples taken from the prior (top) and posterior (bottom) probability distribution. Comparison provides a good idea of those features that are well-resolved (recurring among models) and those that are ill-resolved (non-recurring). From Khan et al. (2004).
Publications
Joint Inversion of Seismic and Gravity Data for Lunar Composition and Thermal State, Khan, A., Connolly, J. A. D., Maclennan, J. and Mosegaard, K., Geophys. J. Int., 168, 243, doi:10.1111/j.1365-246X.2006.03200.x, 2007. [pdf]
Further Constraints on the Deep Lunar Interior, Khan, A. and Mosegaard, K., Geophys. Res. Lett., 32, L22203, doi:10.1029/2005GL023985, 2005. [pdf]
Does the Moon possess a molten core? Probing the deep lunar interior using results from LLR and Lunar Prospector, Khan, A., Mosegaard, K., Williams J. G. and Lognonne, P., J. Geophys. Res., 109, No. E9, E09007, 10.1029/2004JE002294, 2004. [pdf]
An Inquiry Into the Lunar Interior: A Non-Linear Inversion of the Apollo Lunar Seismic Data, Khan, A. and Mosegaard, K., J. Geophys. Res., 107, No. E6, doi10.1029/2001JE001658, 2002. [pdf]
New Information on the Deep Lunar Interior from an Inversion of Lunar Free Oscillation Periods,
Khan A. and Mosegaard, K., Geophys. Res. Lett., 28, 1791, 2001. [pdf]
A New Seismic Velocity Model for the Moon from a Monte Carlo Inversion of the Apollo Lunar Seismic Data, Khan A., Mosegaard K. and Rasmussen, K. L., Geophys. Res. Lett., 27, 1591, 2000. [pdf]
PHEMGP - Computing Physical Rock properties Using phase equilibrium calculations
The use of phase equilibrium calculations to compute physical properties of rocks has become commonplace in geophysical modeling. With PHEMGP (developed by Andrea Zunino in collaboration with myself and James Connolly) we present a computer program that assembles three‐dimensional tables of physico-chemical properties as a function of pressure, temperature and an arbitrary compositional parameter. The input for this program consists of two‐ dimensional tables generated as a function of pressure and temperature by free energy minimization (e.g. PERPLE_X). The code extracts the information from tables and can also be used to convert the information to a form suitable for plotting or further analysis. A simple interpolation routine allows the user to recover information from the three‐dimensional table as a continuous function of its independent variables. We anticipate that the program will be particularly useful for inverse problems, especially for Monte Carlo simulations, where speed of execution is an essential requisite.
Publications
Precalculated phase equilibrium models for geophysical properties of the crust and mantle as a function of composition, Zunino, A., Connolly, J. A. D. and Khan, A., Geochem. Geophys. Geosyst., 12, Q04001, doi:10.1029/2010GC003304, 2011. [pdf]